模拟退火法和爬山法都是启发式算法，也就是说，他们的目的不在于寻找最优解，而是在寻找最优解和成本之间找到平衡。这适用于一些计算机难解问题。比如说旅行商问题。

本文数据下载自： http://comopt.ifi.uni-heidelberg.de/software/TSPLIB95/tsp/a280.tsp.gz
模拟退火的代码： https://gist.coding.net/u/feanor/a8e2351ce0fb44578f7c0181f28bd846
爬山法的代码：https://gist.coding.net/u/feanor/d061dac114fd4b6fb44268bb48da1d0b

读取数据

数据文件前六行为声明、最后一行为EOF字符。中间每行有三个数字：第一个为节点的编号、第二三个为节点的横纵坐标。则读取文件数据的函数可以类似这样：

1
2
3
4
def read_data(filename='../data/a280.tsp'):
    lines = open(filename).readlines()
    line = [line.strip().split() for line in lines[6:-1]]
    return [(int(words[1]), int(words[2])) for words in line]

这样读出了数据的坐标并作为一个列表。

求距离

求距离矩阵以表示节点之间的距离；使用python自带的itertools中的笛卡尔积函数：

1
2
3
4
def distances(points):
    num = len(points)
    distance = [math.sqrt(((x[0] - y[0])**2 + (x[1] - y[1])**2)) for x, y in product(points, points)]
    return np.resize(distance, [num, num])

选取一定数量的点

优化算法都需要说的是，它们并不会比较所有的点，它们只选择其中的一部分进行比较。然后我们就需要构造一个这样的集合：当点的数量多的时候，取得多；点的数量少的时候取得少。这样基本就是正比关系。但是当最后几个数字时候我们则很难取到…：

（说实话，这里的逻辑其实简单粗暴地我不太想写：

1
2
3
4
def get_next(indexs):
    num = len(indexs)
    nextnum = num // 10  if num >= 10 else num
    return random.sample(indexs, nextnum)

爬山法

爬山法的主要逻辑就是给一堆点。然后每次都选取离我最近的点，然后这样我每一步都是最短的，最后遍历完的时候至少也是比较短的点。

1
2
3
4
5
6
7
8
def next_step(distances, curnode, next_list):
    maxcost = 100000
    retnode = 0
    for node in next_list:
        if distances[curnode][node] < maxcost:
            maxcost = distances[curnode][node]
            retnode = node
    return retnode, maxcost

然后算法的主要逻辑如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def hill_climb(distances):
    num = np.size(distances, 1)
    selected = []
    indexs = list(range(num))
    sum_cost = 0

    ## init the loop
    item = random.choice(indexs)
    selected.append(item)
    indexs.remove(item)

    for _ in range(num-1):
        next_list = get_next(indexs)

        curnode = selected[-1] ## the last node of the selected
        nextnode, maxcost = next_step(distances, curnode, next_list)

        sum_cost += maxcost
        indexs.remove(nextnode)
        selected.append(nextnode)
    return selected, sum_cost

模拟退火法

模拟退火法主要逻辑就是不是每个都取最近的点，给概率会接受选取其它的点。然后是对这个概率做文章：最开始这个概率很大，到后来这个就干脆不接受了。这就是模拟退火算法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def next_step(dist, curnode, next_list, temp):
    t_min = 60  ## 最小温度
    max_cost = 100000 ## 初始最大代价
    retnode = 0

    for node in next_list:
        if dist[curnode][node] < max_cost:
            max_cost = dist[curnode][node]
            retnode = node
        else:  ## 有一定概率接受新的节点
            if temp > t_min \
                and math.exp((dist[curnode][node] - max_cost) / temp) > random.uniform(0, 1):
                retnode = node
                max_cost = dist[curnode][node]
                return (retnode, max_cost)
    return (retnode, max_cost)

然后算法的主要逻辑如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def simulate_anneal(distances):
    num = np.size(distances, 1)
    indexs = list(range(num))
    path = []
    sum_cost = 0
    temp = 100

    item = random.choice(indexs)
    path.append(item)
    indexs.remove(item)

    for _ in range(num-1):
        next_indexs = get_next(indexs)

        curnode = path[-1]
        nextnode, maxcost = next_step(distances, curnode, next_indexs, temp)

        # update statement
        temp *= 0.98  ## 退火
        sum_cost += maxcost
        indexs.remove(nextnode)
        path.append(nextnode)
    return path, sum_cost

可视化

因为旅行商问题是遍历所有点的最短路径，所以只要直接将选出的最短路画出来，也就确保所有点都在纸上了。

1
2
3
4
5
6
def pic_visualization(path, points):
    plt.legend()
    x = [points[p][0] for p in path]
    y = [points[p][1] for p in path]
    plt.plot(x, y)
    plt.show()

效果比较

不画图的效率比较

爬山法：

1
2
3
4
5
$ time python tsp.py
最合适的路径为：
 [183, 161, 180, 156, 157, 150, 151, 152, 155, 176, 179, 137, 138, 263, 204, 209, 211, 251, 208, 210, 206, 212, 215, 222, 224, 233, 226, 225, 216, 203, 217, 229, 231, 239, 273, 3, 10, 278, 247, 249, 246, 232, 248, 256, 205, 250, 228, 279, 0, 259, 252, 264, 133, 270, 15, 12, 272, 14, 258, 257, 276, 4, 9, 13, 11, 6, 131, 21, 124, 29, 28, 26, 128, 129, 20, 135, 147, 146, 149, 141, 142, 140, 268, 269, 132, 153, 31, 127, 120, 125, 34, 35, 38, 47, 59, 57, 63, 116, 56, 43, 48, 45, 64, 115, 65, 69, 73, 74, 76, 80, 97, 103, 87, 105, 107, 172, 173, 170, 102, 88, 93, 90, 96, 95, 166, 101, 171, 109, 104, 79, 77, 72, 86, 62, 117, 60, 85, 70, 75, 84, 81, 167, 174, 158, 148, 177, 145, 139, 134, 261, 267, 198, 144, 197, 202, 201, 143, 196, 195, 185, 186, 192, 178, 159, 119, 175, 181, 190, 99, 169, 189, 191, 164, 163, 111, 108, 82, 61, 83, 55, 46, 50, 53, 39, 36, 51, 44, 67, 42, 27, 126, 25, 122, 118, 114, 68, 49, 37, 40, 58, 71, 193, 136, 130, 123, 52, 110, 187, 200, 154, 121, 19, 30, 18, 274, 244, 230, 214, 221, 236, 241, 7, 242, 243, 260, 266, 24, 41, 17, 16, 5, 271, 265, 275, 235, 254, 199, 182, 165, 162, 168, 188, 106, 78, 245, 238, 237, 240, 277, 213, 219, 184, 255, 113, 92, 22, 112, 66, 207, 220, 223, 160, 33, 234, 23, 8, 89, 91, 253, 98, 94, 100, 54, 32, 262, 2, 1, 227, 218, 194]
最小花费为：12272.288796
python3 tsp.py  0.84s user 0.18s system 82% cpu 1.239 total

模拟退火法：

1
2
3
4
5
$ time python tsp.py
最合适的路径为：
[116, 192, 78, 5, 131, 278, 179, 276, 188, 69, 212, 41, 61, 256, 273, 70, 209, 59, 44, 220, 67, 114, 216, 93, 8, 154, 228, 234, 239, 229, 233, 223, 222, 218, 207, 249, 242, 1, 3, 260, 261, 265, 135, 149, 150, 118, 120, 126, 28, 127, 130, 26, 27, 20, 18, 123, 30, 19, 134, 266, 147, 140, 144, 145, 193, 196, 197, 204, 208, 254, 248, 252, 253, 139, 267, 16, 132, 270, 12, 271, 272, 7, 274, 268, 263, 136, 133, 128, 29, 21, 24, 125, 122, 119, 156, 113, 81, 88, 87, 85, 109, 84, 82, 111, 102, 101, 171, 172, 162, 164, 185, 191, 195, 201, 202, 200, 194, 187, 184, 189, 173, 96, 108, 76, 94, 95, 80, 104, 79, 98, 91, 106, 159, 157, 183, 161, 174, 180, 176, 86, 56, 55, 58, 117, 112, 90, 97, 74, 66, 62, 83, 99, 160, 151, 175, 163, 100, 77, 168, 103, 75, 71, 57, 43, 47, 45, 54, 63, 49, 68, 72, 89, 92, 107, 110, 169, 64, 105, 60, 46, 48, 50, 36, 35, 38, 51, 52, 53, 153, 155, 25, 129, 152, 177, 178, 158, 42, 17, 14, 10, 205, 141, 146, 264, 148, 137, 142, 215, 214, 217, 232, 231, 224, 230, 255, 251, 226, 210, 203, 143, 138, 259, 11, 13, 121, 262, 9, 6, 243, 279, 250, 219, 213, 199, 227, 245, 2, 241, 4, 269, 275, 277, 221, 246, 198, 166, 170, 73, 34, 32, 23, 31, 15, 240, 258, 244, 236, 238, 22, 33, 39, 167, 211, 225, 181, 0, 165, 206, 124, 182, 186, 190, 115, 65, 40, 37, 257, 247, 237, 235]
最小花费为：14381.296207
python3 tsp.py  0.92s user 0.27s system 76% cpu 1.560 total

二者产生的路径

爬山法：

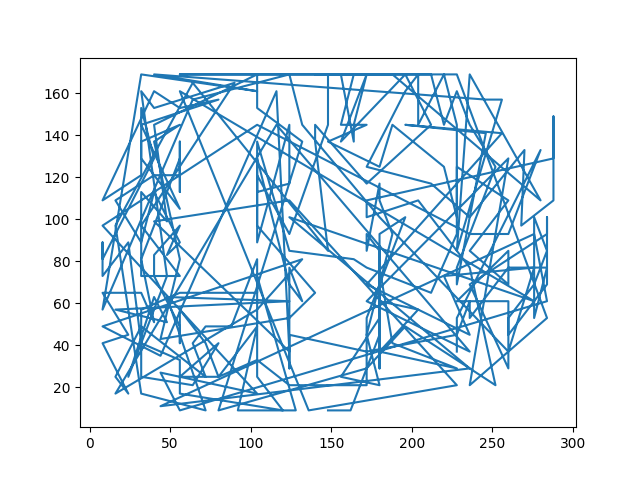
模拟退火法：

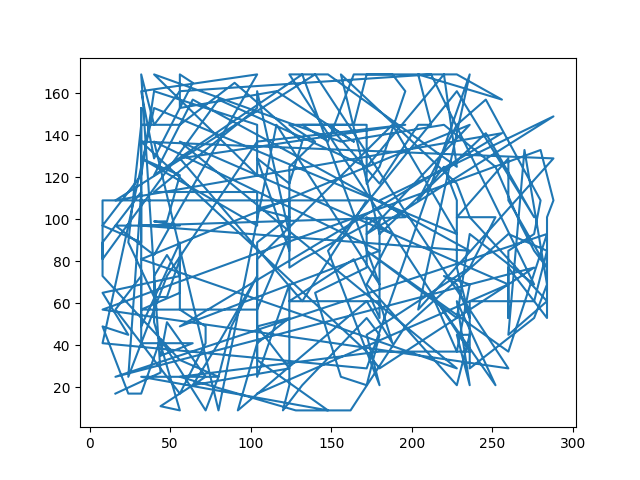
贪心法

贪心法其实跟爬山法是一样的：每次选出最好的结果，但是在贪心法里面是对所有数据进行比较的。

因此它花费的时间会比启发式算法慢，但是它的结果肯定会好不少。这里就用它的结果作为好的对比。

$ python tsp.py
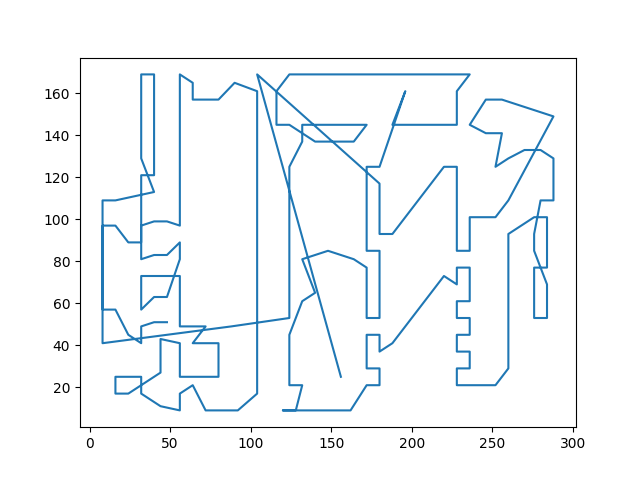
最合适的路径为：
 [108, 88, 80, 79, 78, 75, 74, 73, 72, 71, 70, 69, 66, 65, 64, 63, 62, 61, 117, 60, 59, 42, 41, 40, 39, 38, 37, 36, 35, 34, 33, 32, 30, 29, 124, 123, 122, 121, 120, 119, 118, 156, 157, 158, 159, 174, 160, 161, 162, 163, 164, 165, 166, 167, 168, 100, 99, 98, 97, 92, 93, 94, 95, 96, 91, 90, 89, 103, 102, 101, 169, 170, 171, 172, 105, 104, 106, 107, 109, 110, 113, 112, 86, 83, 82, 81, 87, 111, 114, 116, 115, 85, 84, 57, 56, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 58, 67, 68, 76, 77, 173, 181, 180, 175, 176, 150, 151, 155, 152, 154, 153, 128, 127, 20, 19, 18, 17, 16, 132, 131, 130, 129, 126, 125, 28, 27, 26, 25, 21, 24, 22, 23, 13, 12, 11, 10, 9, 7, 6, 8, 274, 273, 272, 271, 270, 15, 14, 269, 133, 134, 135, 136, 137, 138, 139, 140, 141, 142, 143, 144, 145, 146, 147, 148, 149, 177, 178, 179, 182, 183, 184, 186, 185, 188, 187, 189, 190, 191, 193, 194, 195, 196, 197, 198, 199, 200, 201, 202, 203, 204, 205, 206, 207, 208, 209, 210, 211, 212, 213, 214, 215, 216, 217, 218, 219, 220, 221, 222, 223, 224, 225, 226, 227, 228, 229, 250, 249, 246, 243, 240, 239, 238, 237, 230, 231, 232, 233, 234, 235, 236, 245, 244, 242, 241, 1, 279, 2, 278, 277, 3, 276, 275, 5, 4, 0, 247, 248, 255, 254, 251, 252, 253, 256, 257, 258, 259, 260, 261, 262, 263, 264, 265, 266, 267, 268, 31, 192]
最小花费为：3116.016610

路径可视化：

为什么要写这么一个东西

因为我在网上搜到了一篇错误的教程，里面出现的代码不但错误，而且思想也不对。我愿想做一个更深入地了解的，但是期末已经临近了，博客还是暂时少花一点时间为妙。于是想着就算是纯贴代码也好了，于是就有了这篇博客。如果您也吃过错误教程的亏，您应该会明白我感到愤怒的原因。