一道关于炉石传说的概率题
期末中期在爱数社遇到了这个题,虽然解出来了,但是没有时间将它写成博客,既然今天也是闲的,那就探究一下这个题吧。
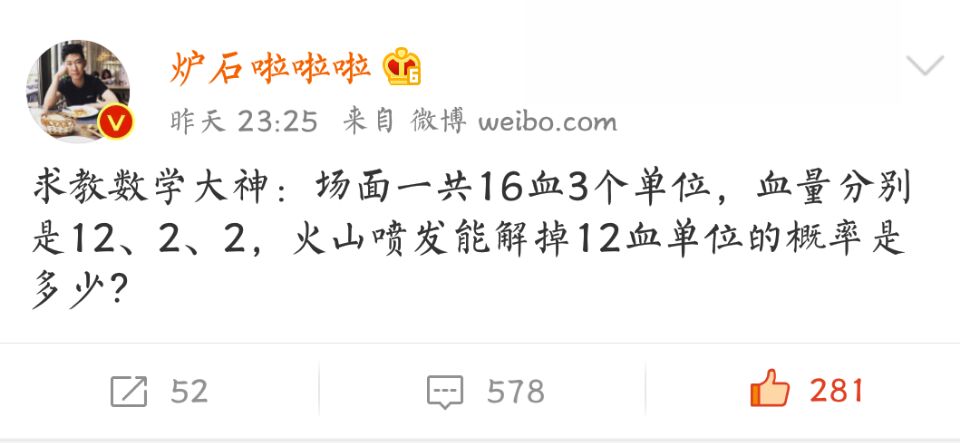
题目是这样的:
想问大家一个问题,我今晚想了好久了。我喜欢玩炉石传说,这是我今晚看直播遇到的真事。有一张牌,叫火山喷发,造成15点伤害,随机分配到所有随从身上,15点是一下一下打上去的,每一下都随机。场上有三个随从,分别是12血,2血,2血,也就是说最后只会剩一个1血的随从,问火山喷发打死12血随从的概率是多少?
炉石传说我没玩过,但是看描述背景应该是剩下n个随从的时候,每一个随从被打击的概率是$1/n$。
分析法
我是直接求的概率,这种方法第一次算的时候还出错了。我算的是剩下12血随从的概率是多少。
首先我们将这个过程分为3个阶段,一个是剩3个随从的阶段,一个是剩2个随从的阶段,最后是只剩一个随从的阶段。最后阶段的时候,打击必然落在最后的随从的身上,概率为1。所以我们只考虑一二阶段:
第一阶段
情况1:剩下一名原12血的随从和一个仍为2血的随从。假设此阶段打击了m1次
即我们有两次打击落在了一名随从上,而且最后一击将该随从打死。在$m1-1$次打击中选出1次打击到死亡的二血随从上,其他都是打到12血随从上。
$$
P_{m1} = \left( frac{1}{3} \right)^{m1} C_1^{m1-1}
$$
需要注意的是:这两名随从是可以任取的,所以这个结果要乘2。
情况2:剩下一名一血随从和12血随从。假设此阶段打击了n1次。
即我们有两次打击落到了两名2血随从身上。然后最后一击将其中一名随从打死。就是选两次让他们落到特定的随从上,然后这两次落到的顺序任取。
$$
p_{n1} = \left( frac{1}{3} \right)^{n1} C_2^{n1-1} A_2^2
$$
第二阶段
情况一:对应第一阶段的情况一。假设这里的打击次数是m2。
剩下有两次打击落在原2血的随从上。从最后一次打击前的m2-1次中选出1次即可。
$$
p_{m2} = \left( frac{1}{2} \right)^{m2} C_1^{m2-1}
$$
情况二:对应第一阶段的情况二。假设这里的打击次数是n2。
剩下有1次打击落在原2血的随从上。直接取最后一次即可。
$$
p_{n2} = \left( frac{1}{2} \right)^{n2}
$$
则总的12血存活的概率是:
$$
p = p_{m1}p_{m2} + p_{n1}p_{n2}
$$
则其死亡的概率也就可以求了
写一个程序来计算这个:
1 |
|
程序直接模拟法
有同学用的深度搜索直接模拟的。
1 |
|
答案是0.00336842。
不过最佳答案是非洲人0%,欧洲人100%。好了下一题